Obra científica
Después de estudiar teología en la universidad de Tubinga, incluyendo astronomía con un seguidor de Copérnico, enseñó en el seminario protestante de Graz. Kepler intentó comprender las leyes del movimiento planetario durante la mayor parte de su vida. En un principio Kepler consideró que el movimiento de los planetas debía cumplir las leyes pitagóricas de la armonía. Esta teoría es conocida como la música o la armonía de las esferas celestes. En su visión cosmológica no era casualidad que el número de planetas conocidos en su época fuera uno más que el número de poliedros perfectos. Siendo un firme partidario del modelo copernicano, intentó demostrar que las distancias de los planetas al Sol venían dadas por esferas en el interior de poliedros perfectos, anidadas sucesivamente unas en el interior de otras. En la esfera interior estaba Mercurio mientras que los otros cinco planetas (Venus, Tierra, Marte, Júpiter y Saturno) estarían situados en el interior de los cinco sólidos platónicos correspondientes también a los cinco elementos clásicos.
En 1596 Kepler escribió un libro en el que exponía sus ideas. Misterium Cosmographicum (El misterio cósmico). Siendo un hombre de gran vocación religiosa, Kepler veía en su modelo cosmológico una celebración de la existencia, sabiduría y elegancia de Dios. Escribió: «yo deseaba ser teólogo; pero ahora me doy cuenta a través de mi esfuerzo de que Dios puede ser celebrado también por la astronomía».
En 1600 acepta la propuesta de colaboración del astrónomo imperial Tycho Brahe, que a la sazón había montado el mejor centro de observación astronómica de esa época. Tycho Brahe disponía de los que entonces eran los mejores datos de observaciones planetarias pero la relación entre ambos fue compleja y marcada por la desconfianza. No será hasta 1602, a la muerte de Tycho, cuando Kepler consiga el acceso a todos los datos recopilados por Tycho, mucho más precisos que los manejados por Copérnico. A la vista de los datos, especialmente los relativos al movimiento retrógrado de Marte se dio cuenta de que el movimiento de los planetas no podía ser explicado por su modelo de poliedros perfectos y armonía de esferas. Kepler, hombre profundamente religioso, incapaz de aceptar que Dios no hubiera dispuesto que los planetas describieran figuras geométricas simples, se dedicó con tesón ilimitado a probar con toda suerte de combinaciones de círculos. Cuando se convenció de la imposibilidad de lograrlo con círculos, usó óvalos. Al fracasar también con ellos, «sólo me quedó una carreta de estiércol» y empleó elipses. Con ellas desentrañó sus famosas tres leyes (publicadas en 1609 en su obra Astronomia Nova) que describen el movimiento de los planetas. Leyes que asombraron al mundo, le revelaron como el mejor astrónomo de su época, aunque él no dejó de vivir como un cierto fracaso de su primigenia intuición de simplicidad (¿por qué elipses, habiendo círculos?). Sin embargo, tres siglos después, su intuición se vio confirmada cuando Einstein mostró en su Teoría de la Relatividad general que en la geometría tetradimensional del espacio-tiempo los cuerpos celestes siguen líneas rectas. Y es que aún había una figura más simple que el círculo: la recta.
En 1627 publicó las Tabulae Rudolphine, a las que dedicó un enorme esfuerzo, y que durante más de un siglo se usaron en todo el mundo para calcular las posiciones de los planetas y las estrellas. Utilizando las leyes del movimiento planetario fue capaz de predecir satisfactoriamente el tránsito de Venus del año 1631 con lo que su teoría quedó confirmada.
Escribió un biógrafo de la época con admiración, lo grande y magnífica que fue la obra de Kepler, pero al final se lamentaba de que un hombre de su sabiduría, en la última etapa de su vida, tuviese demencia senil, llegando incluso a afirmar que "las mareas venían motivadas por una atracción que la luna ejercía sobre los mares...", un hecho que fue demostrado años después de su muerte.
En su honor una cadena montañosa del satélite marciano Fobos fue bautizada con el nombre de 'Kepler Dorsum'.
G
A.1571
B.1775
C.1567
¿SU OBRA REPRESENTATIBA ES?
A.Polidros perfectos
B.el onfonoto
C.Finito









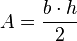


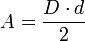
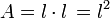






 . Matemáticamente se dice que dicha función es una onda si verifica la ecuación de ondas:
. Matemáticamente se dice que dicha función es una onda si verifica la ecuación de ondas: